Almost every graphics game developer I’ve met knows Schlick’s approximation for Fresnel reflectance. This approximation has all the features to be well used in games. It looks visually equivalent to the real Fresnel computation for unpolarized light, while being way easier to compute. However, very few developers have actually looked at Christophe Schlick’s original 1994 Computer Graphics Forum paper, “An Inexpensive BRDF Model for Physically-based Rendering“. That is a shame, because this paper has some really good ideas for coming up with other approximations for shader computation.
The basic idea is to come up with a rational function (ratio of two polynomials) as an approximation. There’s a long history of this in and out of graphics, but it usually has some inherent problems. Consider “Fast Phong Shading“, published by Bishop and Weimer in SIGGRAPH 1986. This method attempts to avoid the vector renormalization inherent in Phong normal interpolation by using a quadratic Taylor series. Unfortunately, Taylor expansion is inherently centered around a point, in this case the center of the triangle. The approximation will have some error by the time you get to the edge of the triangle, and two triangles sharing that edge won’t necessarily have the same amount of error in their normalization. For big triangles, this can result in a visible shading discontinuity along trangle edges. Not good.
Schlick’s idea is to express what’s important about any function as kernel conditions, then apply those as constraints. For his Fresnel approximation
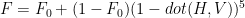
These constraints are that F should be 1 when dot(H,V)=0, F0 when dot(H,V)=1, and the first several derivatives of F should also be 0 when dot(H,V)=1. In the paper, he also has similar approximations for the geometric attenuation and distribution terms of a Cook-Torrance shading model, but the method is a good one to know in general for reducing shader computation:
- Look at the function and pick the kernel conditions: value or derivatives at some critical points, desired integral over the whole domain, etc.
- Based on the way the function looks, choose a rational function with the right number of coefficients. This is still somewhat of a black art, since there will be many choices for numerator and denominator polynomial that have the same number of coefficients as you have kernel conditions. For example, for four conditions, you could choose a cubic, quadratic numerator/linear denominator, linear numerator/quadratic denominator, or 1/cubic denominator.
- Solve for each coefficient
- Evaluate the total error, decide if it is good enough. If not, try a different rational function, or add extra kernel conditions to fix the problem.
Multi-variate functions are OK, though will potentially introduce many additional coefficients. This kind of approximation is usually best applied near the visual output end of a shader. Applied to computation too early on, and the small errors may be magnified by the intervening shader code. None the less, it can be a great way to reduce a computationally expensive shader.




