Short one today, just a note on nonlinear transformations. The usual translations, rotations and scaling transformations can all be described as a linear transformation (= matrix multiply). Even linear blend skinning, which blends between per-bone linear transformations is effectively piecewise linear. That basically means that each of x,y,z and w after transformation depend only on linear terms of x,y,z and w before transformation:

p1.x = a p0.x + b p0.y + c p0.z + d p0.w

Anything that includes higher powers of x,y,z or w, or some non-linear function is a nonlinear transformation:

p1.x = a2 p0.x p0.x + a1 p0.x + b p0.y/p0.w + c sin(p0.z)

I haven’t seen nonlinear transformations used too much in real-time graphics. There have been a few non-linear extensions to the linear blend skinning and some approaches for generating non-linear environment maps (e.g. paraboloid maps). They were popular for a time for free form deformation for production animation.

None the less, understanding what happens to points, tangents and normals helps explain where some of the well-known rules of graphics originate.

First, assume we’re transforming p0 to p1 by some function f:

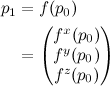
\begin{align*} p_1 & = f(p_0) \\ & = \begin{pmatrix} f^x(p_0) \\ f^y(p_0)\\ f^z(p_0) \end{pmatrix} \end{align*}

According to the rules of differential geometry, surface tangent vectors should transform by the Jacobian of the transform. The Jacobian is a matrix of partial derivatives (which I’ll indicate by subscripts, making my choice to label the components with superscripts above make a little more sense)

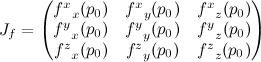
J_f=\begin{pmatrix} {f^x}_x(p_0) _y(p_0) _z(p_0) \\ {f^y}_x(p_0) _y(p_0) _z(p_0) \\ {f^z}_x(p_0) _y(p_0) _z(p_0) \\ \end{pmatrix}

It depends on where p is, but it’s still just a matrix, so this is just a matrix multiply. I like to write tangent vectors as columns, so the multiply would look like this

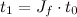
t_1 = J_f \cdot t_0

Also, according to the rules of differential geometry, surface normal vectors should transform by the inverse Jacobian. I like to write normal vectors as rows, in which case the multiply would look like this:

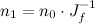
n_1 = n_0 \cdot J_f^{-1}

One property of this is that the dot product of a normal and tangent are not affected by the transformation from one space to another (which is good):

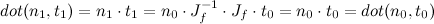
dot(n_1,t_1) = n_1 \cdot t_1 = n_0 \cdot J_f^{-1} \cdot J_f \cdot t_0 = n_0 \cdot t_0 = dot(n_0,t_0)

What does this have to do with ordinary linear transforms? Assuming no perspective, a linear transform looks something like this:

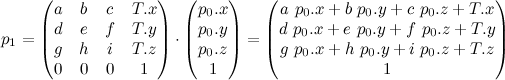
p_1 = \begin{pmatrix} a & b & c & T.x \\ d & e & f & T.y \\ g & h & i & T.z \\ 0 & 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} p_0.x \\ p_0.y \\ p_0.z \\ 1 \end{pmatrix} = \begin{pmatrix} a\ p_0.x + b\ p_0.y + c\ p_0.z + T.x\\ d\ p_0.x + e\ p_0.y + f\ p_0.z + T.y\\ g\ p_0.x + h\ p_0.y + i\ p_0.z + T.z\\ 1 \end{pmatrix}

Dropping the constant row, the Jacobian of that guy is:

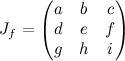
J_f = \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{pmatrix}

So that’s where “transform vectors by the upper left 3×3 corner of the transformation matrix” comes from. Similarly, we can understand transforming normals by the inverse transpose: inverse because it’s the inverse Jacobian, and transpose so you can multiply as a column on the right rather than a row on the left.

But… now we know how to do other nonlinear transforms, including what to do if this matrix actually has some perspective in it. Build a Jacobian matrix.

[Originally, this post attempted to use html for the math, which sucked. Updated to use LaTeX + MathURL]